Die Simulation von mathematisch beschreibbaren Prozessen ist für viele Anwendungen nützlich. Die „Monte-Carlo-Simulation“ ist eine elegante Methode, verschiedene Probleme zu lösen, etwa die Berechnung der Kreiszahl Pi.
RapidMiner wird zwar nicht unbedingt als Simulationswerkzeug beworben, aber auch diese Aufgabe läßt sich mit etwas Know-How leicht darin lösen. Und was liegt näher als die „Monte-Carlo-Simulation“ am Beispiel von (französischem) Roulette zu demonstrieren?
Roulette läßt sich einfach beschreiben: Die Spieler setzen auf verschiedene Bereiche eines Tisches. Diese Bereiche decken unterschiedlich große Teile des Zahlenraums zwischen 0 und 36 ab. Die Wahrscheinlichkeit, daß ein Zahlenfeld gewinnt, liegt bei 1/37; bei größeren Bereichen (z. B. vier Zahlen, sechs Zahlen, ein Drittel der Zahlen von 1-36, eine Farbe) bei Mehrfachen davon. Der Gewinn ist bei einzelnen Zahlen das 35-Fache des Einsatzes (zusätzlich zum Einsatz, den man behält), und nimmt bei größeren Bereichen proportional zum Risiko ab. Z. B. erhält man, wenn man etwa auf Rot gesetzt hat und die Kugel auf einem roten Feld landet, den Einsatz noch einmal zurück. Da auch das Feld 0 existiert, das von den meisten möglichen Einsätzen nicht abgedeckt ist, verdient die Bank auch manchmal Geld. Roulette ist wahrscheinlich das „fairste“ reine Glücksspiel, das man spielen kann. (Deswegen gibt es wohl auch „Amerikanisches Roulette“ mit einem zweiten Null-Feld – Die Kasinos in den USA haben sich mit 1/37 Gewinn nicht zufriedengegeben.)
Simulationsprozess
Der hier verfügbare Prozess simuliert wiederholte Besuche im Kasino mit einigen Einstellungen. Die Einstellungen lassen sich im Prozesskontext (View/Show Panel/Context) in Form von Makros setzen. Sie sind auch direkt im Prozess beschrieben.
Man legt die Anzahl der Besuche fest und die Anzahl der Spiele pro Besuch (solange man noch Geld übrig hat). Es läßt sich auch ein Betrag angeben, bei dessen Erreichen man freiwillig aufhört zu spielen. (Z. B. wenn man das anfängliche Guthaben verdoppelt hat.)
Die eigene Spielweise läßt sich im Makro „Risk“ einstellen. Hier legt man das gewünschte Risiko fest: von 2 (rot/schwarz, gerade/ungerade, 1-18/19-36) bis 36 (einzelne Zahl).
Der Prozess besteht aus zwei verschachtelten Schleifen (Loop Visits und Loop Bets) und danach etwas Datenaufbereitung für die Darstellung der Ergebnisse.
Die tatsächliche Berechnung einer Spielrunde findet in „Calculate bet results“ (Generate Attributes) statt. Aus dem Einsatz und dem Risiko wird der Gewinn (Einsatz + gewonnener Betrag) oder der Verlust (der Einsatz) berechnet; daraus dann das neue Spielguthaben.
Nach der Ausführung der äußeren Schleife werden Kennzahlen errechnet.

average(VisitWonPct): Anteil des Einsatzes, der durchschnittlich gewonnen oder verloren wurde. (Realistischerweise eher verloren, ausgedrückt durch eine negative Zahl.)
average(VisitReachedGoal): Anteil der Casino-Besuche, bei denen man das Ziel-Guthaben (z. B. 150 € bei einem Anfangsguthaben von 100 €) erreicht hat.
average(VisitLostEverything): Anteil der Casino-Besuche, bei denen man das gesamte Anfangsguthaben verloren hat.
average(VisitWonAmount): Durchschnittlich gewonnener oder verlorener Betrag.
Zusätzlich lassen sich die Verläufe der einzelnen Besuche grafisch darstellen:
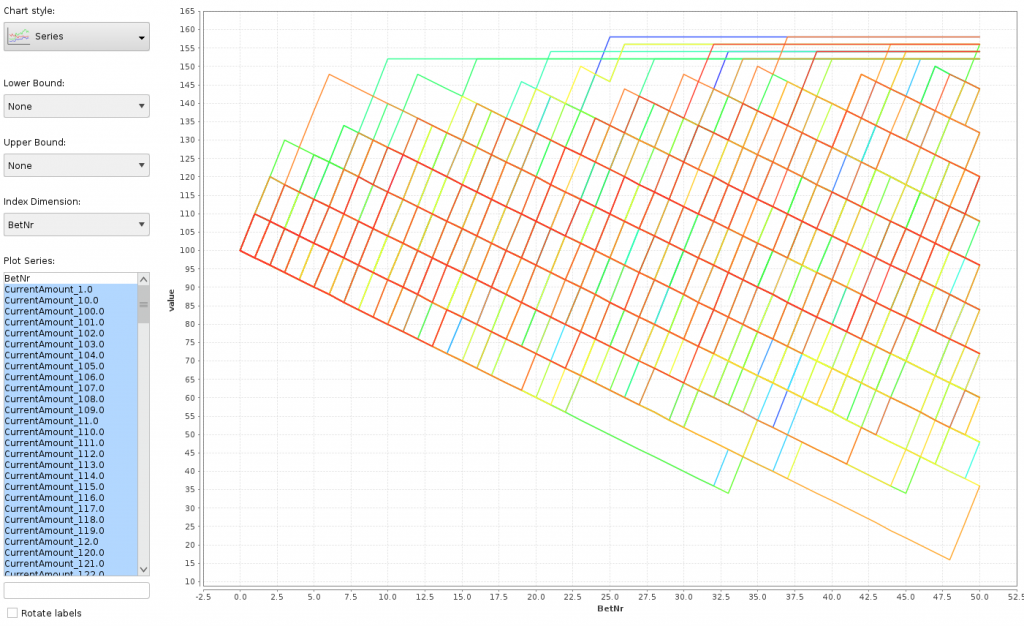
Dafür habe ich das Ergebnis „Pivot for series plot“ geöffnet, die Charts aktiviert, den Chart-Typ Series ausgewählt, die BetNr als Index-Dimension festgelegt und alle CurrentAmount-Spalten für die Plot Series markiert.
Jede Linie zeigt den Verlauf eines Casinobesuchs (pro Besuch eine Farbe). Die X-Achse ist die Spielrunde, die Y-Achse das Guthaben, das man nach dieser Runde hat. Es ist gut sichtbar, daß es Besuche gab, in denen man über 30 Runden nur verloren hat! Oben ist das Feld durch die Besuche begrenzt, in denen man vor Ablauf der geplanten Spielrunden den Zielbetrag erreicht hat.
Mit diesem Simulationsprozess, der auch mit RapidMiner Studio Basic (gratis und ohne Registrierung nutzbar) funktioniert, läßt sich gut feststellen, wie die Chancen im Casino stehen, wenn man mit einer „Strategie“ spielt. Wenig überraschend ist das Ergebnis überwiegend negativ.
Der Prozess ließe sich leicht für andere Arten von Spielen und generell andere Zwecke adaptieren. Eine Monte-Carlo-Simulation zur Annäherung von Pi wäre z. B. mit der gleichen Struktur möglich.
Simulation in RapidMiner
There are many applications for simulation of processes that can be described mathematically. The Monte Carlo simulation is an elegant method for solving different problems like calculating Pi.
RapidMiner is not advertised as a simulation tool, but with a bit of knowledge you can easily solve this task in it. So how about demonstrating Monte Carlo simulation with the example of French roulette?
The game of roulette is easy to describe. Players bet on different areas of a table. The areas cover smaller or larger sets of the numbers between 0 and 36. The probability of winning with a single number is 1/37; when betting on a larger area (e. g. four numbers, six numbers, one third of the numbers between 1 and 36, one color) it is a multiple of that. The won amount when guessing a number correctly is the 35 times the bet amount (and the player keeps the bet), and it decreases proportionally with the risk. For example, if you bet on red and the ball lands on a red field, you win an equal amount to your bet.
There is also a field with 0 that is not covered by most of the bets, so the bank also wins sometimes. Roulette is probably one of the most „fair“ games of luck available. (That’s probably the reason for the existence of American roulette that has a second 0 field: The US casinos weren’t satisfied with winning just 1/37 of the players‘ money.)
Simulation process
The process available here simulates repeated casino visits with a few settings. You can manipulate the settings in the process context (View menu/Show Panel/Context) in the Macros area. The process contains a description of each setting.
You can specify the number of visits and the betting rounds per visit (as long as there’s money left in the current visit). It is also possible to specify an amount that is enough to leave the casino before the specified number of rounds. (E. g. when you doubled the original amount.)
You can set a „style of gambling“ with the macro „Risk“. Here you specify the risk you’d like to try: it starts at 2 (red/black, even/odd, 1-18/19-36) and ends at 36 (betting on one number).
The process contains two loops, the first one (Loop Visits) holding the second one (Loop Bets) inside. After those there is some processing for displaying results.
The calculation of one betting round happens in „Calculate bet results“ (Generate Attributes). The amount lost or won in the round is calculated from the bet amount and the risk. This results in a change of the current amount.
After finishing the outer loop, the process calculates a few summary results.

average(VisitWonPct): Portion of the original amount that was lost or won in the average case. (Realistically, lost: this is expressed with a negative percentage.)
average(VisitReachedGoal): Portion of visits when reaching the desired amount (e. g. 150 € after starting with 100 €).
average(VisitLostEverything): Portion of visits when you lost everything.
average(VisitWonAmount): Average amount won or lost.
In addition to the numbers you can display each visit graphically:

Open the „Pivot for series plot“ result, go to Charts, select Series, select BetNr as the Index dimension and mark all CurrentAmount attributes as Plot Series.
Each line describes the course of a casino visit (one color per visit). The X axis is the betting round, the Y axis the available amount after the round. It is easy to see that in several visits up to 30 rounds have been lost! The upper limit is the specified „leaving amount“ that was reached before the number of specified rounds.
This simulation process even works in RapidMiner Studio Basic (available for free without registration). You can easily determine your chance of winning in the casino playing your „strategy“. It’s not a big surprise that the result is mostly negative.
It should be easy to change the process to simulate other games or events. For example, you could estimate Pi using the same process structure.